Why we can't see a magnetic monopoles

A magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole (a north pole without a south pole or vice-versa). In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring theories, which predict their existence. Magnetism in bar magnets and electromagnets does not arise from magnetic monopoles, and in fact there is no conclusive experimental evidence that magnetic monopoles exist at all in the universe. One of Maxwell's equations, so called Gauss's law for magnetism, is the mathematical statement that there are no magnetic monopoles. As has been showed by Dirac, the theoretical reciprocity between electricity and magnetism is perfect and Dirac showed that if any magnetic monopoles exist in the universe, then all electric charge in the universe must be quantized. 

Good question is, why we can not observe such magnetic monopoles in contrast with electric monopoles? 

Why Nature select not symetrical definition of Maxwell equations? div B = 0 vs. div E = notzero.

Starting from this we can write well known Maxwell's equations, which are invariant under Lorentz transformation. The Lorentz transformations are the isometries which leave the origin fixed. The Lorentz group is a subgroup of the Poincare group, the group of all isometries of Minkowski space-time. Because the restricted Lorentz group SO+(1, 3) is isomorphic to the Moebius group PSL(2,C), its conjugacy classes also fall into four classes: a) elliptic transformations, b) hyperbolic transformations, c) loxodromic transformations, d) parabolic transformations.

Hyperbolic transformation generate from electromagnetic four potential a time space derivation of scalar potential and time derivation of vector potential. This is a definition for electric intensity vector E.

Elliptic transformation generate from electromagnetic four potential antisymmetric space derivation, rotation of vector potential. This is a definition for magnetic induction vector B.

Graphical effect of such transformation after stereographics projection give as visual reason why nature select rule that div B = 0 , magnetic fields (eliptic Moebius transformations) have not a monopoles in plane projection. If our universe is hyperplane from such conformal projection of more symmetric and more dimensional structure, we have mechanism to explain reason, why we can not see magnetic monopoles.

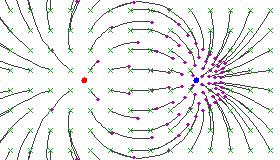
For hyperbolic Moebius transformation after stereographics projection we can see force curves flow generated via monopoles, picture typical for electric charge.

Sources of pictures:

https://en.wikipedia.org/wiki/M%C3%B6bius_transformation

http://physics.stackexchange.com/questions/143119/why-in-a-solenoid-do-the-magnetic-field-lines-resemble-that-of-a-bar-magnet